Calorimetry: Heat of Neutralization Reaction & Hess's Law

Introduction

Measuring the energy produced or consumed by a reaction can be as important as analyzing the reactants and products. In the lab today, you and a partner will find out the molar heat of reaction given off by the acid-base neutralization reaction between hydrochloric acid and sodium hydroxide under two different conditions:

HCl(aq)   + NaOH(aq)    ==> NaCl(aq)  + H₂O                H_{rxn 1} = ?

HCl(aq)   + NaOH(s)    ==> NaCl(aq)  + H₂O                  H_{rxn 2} = ?

You will also measure the molar heat of reaction generated from the dissolution of solid sodium hydroxide in water,

NaOH(s) ==> NaOH(aq)                                                 H_{rxn 3} = ?

Hess's law states that the enthalpy change of an overall process is the sum of the enthalpy changes of its individual steps.  Notice that the above listed reaction 3 and reaction 1 together can be considered as alternative steps to reaction 2. Thus, when the solution concentrations of NaOH and HCl are controlled to be the same in all three reactions, we can expect 

H_{rxn 1} +  H_{rxn 3} =  H_{rxn 2}  

Experimentally, you will use a simple solution calorimeter constructed of nested Styrofoam cups, a cardboard lid and a thermometer. Styrofoam is a good insulator, even though some heat will be absorbed by the cups and some will be released to the surroundings, it is small enough as compared to the heat absorbed by the solution in the calorimeter.  Thus, in this experiment, we will consider the heat absorbed by the cup, lid, thermometer and the rest of  the surroundings negligible. 

Figure 1. The components of a Calorimeter --- nested cups, thermometer and lid

When measuring the Heat of Reaction, we mix roughly equal moles of HCl solution and NaOH  in the calorimeter and measure the temperature change of the solution inside the calorimeter.  The law of conservation of energy is the basis for calculation for reaction heat (Remember that we assumed that there was no heat lost to the surrounding through the calorimeter setup),

                                                         q_rxn + q_soln = 0                                                 (1)

where q_rxn is the heat generated by the reaction (it should be negative in value, why?), q_soln is the heat absorbed by the solution which is reflected by the temperature change.

q_soln can be calculated from the following,

                                                     q_soln = m_soln C_soln T                                            (2)

where is m_soln is the mass, C_soln is the specific heat capacity, and T is the temperature change of the final reaction solution.

The q_rxn can be determined by

                                                           q_rxn = -q_soln                                                      (3)

The above q_rxn is the measured experimental heat of reaction for the amount of HCl/NaOH you are using in this experiment, We can convert it to a measured molar heat of reaction through dividing the q_rxn by the mole value of the smaller of the NaOH moles or HCl moles used in the reaction. 

Note: A majority of the experimental data you are taking in the lab are temperature readings.  It takes additional analysis and graphing for you to be able to determine the "T’s needed in your calculations. Thus, refer to the additional data treatment section at the end of the lab.

Procedure

CAUTION: NaOH is extremely corrosive. Prevent its contact with your skin or eyes.  HCl is a strong acid.  Again, prevent contact.

A. Heat of Reaction : HCl_(aq) + NaOH_(aq) ==> NaCl_(aq) + H₂O_(l)

1. With a 100-mL graduated cylinder, measure 75 mL of 2.0 M HCl and transfer it into the nested reaction calorimeter cup, Rinse and dry the graduated cylinder and then measure a equal volume (75 mL) of 2.0 M NaOH  and transfer it into a 150-mL beaker.

2. Measure and record the temperature of each solution.

3. On a time signal from one partner, the other partner should completely pour the NaOH solution into the reaction calorimeter cup.

4. Use the thermometer through the lid to briefly stir the two solutions until you achieve thorough mixing.

5. Keep the lid firmly in place, and measure the temperature of the solution every 30 seconds.

6. Continue stirring and recording the temperature until the temperatures reach a maximum and remain constant or decrease smoothly for five consecutive readings.

7. Calculate the heat of reaction assuming the volume, the density and the specific capacity of the solution to be 150. mL,  1.02 g/mL and 4.00 J/g^oC. 

8. Run the above procedure again. Then average the two heats of reactions obtained.

B. Heat of Reaction: HCl_(aq) + NaOH_(s) ==> NaCl_(aq) + H₂O_(l)

1. Mix 80 mL of 2.0 M HCl and 70 mL of distilled water in the calorimeter. Measure and record the temperature of this diluted acid solution.

2. Quickly weigh out using a stoppered 125 mL flask as a weighing bottle. On a time signal add  all 6.00 g of solid sodium hydroxide into the calorimeter. (NaOH is hygroscopic, and will absorb enough water from the air to change its apparent mass if left exposed to the air for long.)

3. Stir vigorously but not to splatter solution onto the lid or outside the cup. And continue to record temperature readings as in par A until a maximum has been reached and remain constant or decrease smoothly for five consecutive readings.

4. Calculate the heat of reaction assuming the volume, the density and the specific capacity of the solution to be 150. mL,  1.02 g/mL and 4.00 J/g^oC. 

5. Run the above procedure again. Then average the two heats of reactions obtained.

C. Heat of Solution:  NaOH_(s) ==> NaOH_(aq)  

1. Measure 150 mL of distilled water into the calorimeter. Measure and record the temperature. 

2. Quickly weigh out 6.00 g of solid sodium hydroxide.

3. On a time signal drop the NaOH pellets into the water in the calorimeter.

4. Stir vigorously with the thermometer. (You want to insure that the pellets dissolve as soon as possible, but you don’t want to break the thermometer!)

5. As before, start timing at the moment of adding the pellets, and record the temperature every 30 sec until the values reach a maximum and either remain constant or decrease smoothly for five readings.

6. Run the above procedure again. Then average the two heats of reactions obtained.

Additional Data Treatment

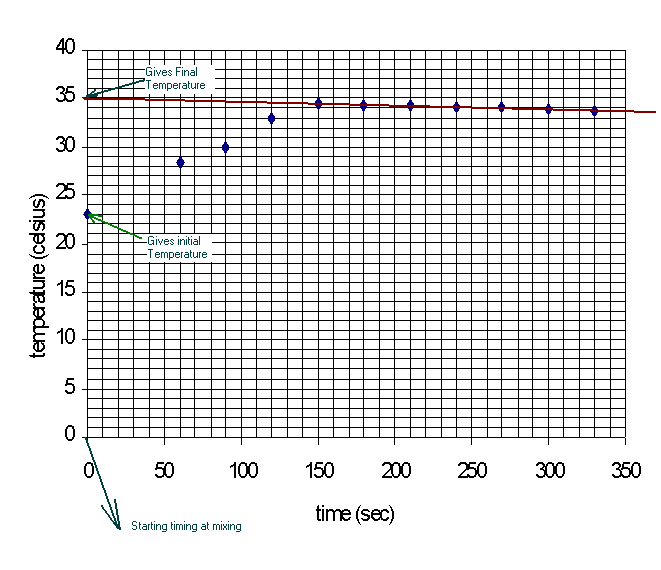
Although time is a set of data that we took in our lab procedures, it is not a factor in the equations we used for our calculations mention in the introduction section.  This is because we assumed heat was instantly exchanged at the time of mixing.  Thus, the "T"s we use in our calculations are the "T"s at mixing time.  Notice that no reasonable temperature readings can be taken at the time of mixing, therefore we need to use the smooth trends in our data over time to estimate the temperatures at mixing by extrapolation.  Below are example diagrams of the graphs you need to draw to get the correct initial and final temperatures for the T calculations.

  Figure 3. Typical Reaction Temperature Profile