Measurement, Calculation, and Error
In reports of scientific work, each quantity has two parts: a numerical value and a unit of measure. In a laboratory context, the word error refers not to a mistake, but to
your degree of confidence in a reported value. The precision of measured values
(and calculations based on those measured values) is limited by the nature of
the system measured and the tools used to make the measurements.
Reading
digital instruments: Record all
digits. For example, if a balance display reads 27.100 g, write 27.100 g, not
27.1 g.
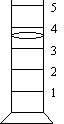
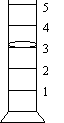
Reading
linear instruments: Read and record
to 0.1 of the smallest division. When using a graduated cylinder whose
smallest division is 1 mL, record to 0.1 mL.
![]()
![]()
Retain
extra digits measured or shown on your calculator until all calculations of a value
are complete, then round to the correct number of significant figures (# s.f.).
See the discussion of significant figures in your lecture text (Chang, Chapter 1).
Example: The
mass of a 10.00 mL sample of liquid is 10.176 g.
Density = 1.0176 g/mL, rounds to 1.018 g/mL (4 s.f.)
Absolute Error is the absolute value of the difference
between the true value (or expected value) and your measured or calculated
value.
Absolute Error = |True Value – Found
Value|
Relative Error is the absolute error expressed as a
fraction of the true value.
Relative Error =
Percent Error is the relative error expressed as a
percentage of the true value.
Percent
Error = Relative Error x 100% = x 100%
The Range is the difference between the
largest and smallest measured or calculated value of a quantity.
Examples:
1. Three measurements of the density of a
solution give values of 1.017, 1.016, and 1.020 g/mL. The average of these
values, taken as the found value, is 1.018 g/mL. The true value of the density
is known to be 1.020 g/mL. Calculate the absolute error, the relative error,
the percent error and the range.
Absolute Error = |1.020 – 1.018| = 0.002
g/mL
Relative Error = = 0.0019607 = 0.002
Percent Error =
Relative Error x 100% = 0.19607% = 0.2%
Range = 1.020 –
1.016 = 0.004 g/mL
2. The
percentage of SrCl2.6H2O
in a mixture is found to be 61.2%. The true value is 60.1%. Calculate the
absolute error, the relative error and the percent error.
Absolute Error =
|60.1 – 61.2| = 1.1%
Relative Error = = 0.0183028 = 0.018
Percent Error = x 100%= 1.83028% = 1.8%