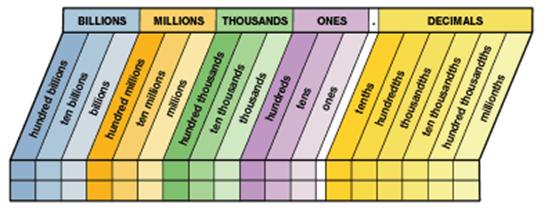
Section 3.1 Decimal Notation, Order, Rounding.

Recall that mixed numerals represent a combination of an integer and fractional parts. There is another way to represent the numbers that are parts of integers, this number representation is called decimal notation.

One of the examples of the decimal numbers used in everyday life is money. Parts of the dollars (pennies) are represented in decimal notation:

$1.25, $0.39, $4.50, $6.07

In decimal notation the integer part is separated from the fractional part by the decimal point.

Example:

The number in decimal notation is an alternative way of writing a number with the fractional part:

or

To Write a Word Name from Decimal Notation

1. Write a word name for the number named to the left of the decimal point

2. Write the word “and” for the decimal point

3. Write a word name for the number on the right of the decimal point, followed by the place value of the last digit

359.247 is read as

Three hundred fifty nine and two hundred forty seven thousandths

Example:

a. Read the number 306.7541

Three hundred six and seven thousand five hundred forty one ten thousandths

b. Read the number 35.07

Thirty five and seven hundredths

c. Read the number 5.917

Five and nine hundred seventeen thousandths

Converting from Decimal to Fraction Notation and Back

Example:

Write a decimal in a fraction notation

a.

b.

To Convert from Decimal to Fraction Notation

a. Count the number of decimal places

b. Move the decimal point that many places to the right

c. Write the result over a denominator with 1 followed by that many zeros

Example:

Write a decimal in a fraction notation

a.

b.

c.

To Convert from Fraction to Decimal Notation when Denominator is

10, 100, 1000 and so on…

a. Count the number of zeros

b. Move the decimal point that many places to the left. Leave off the denominator

Example:

Write a fraction in a decimal notation

a. two zeros in denominator

b.

Write a fraction in a decimal notation

a. 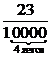two zeros in denominator

b.

Order.

Example:

Compare two numbers in decimal notation 0.35 and 0.4

If we write both numbers in fraction notation, we can compare the fractions:

Since

Comparing Positive Decimals

To compare two positive numbers in decimal notation, start at the left and compare corresponding digits moving from left to right. If two digits differ, the number with the larger digit is the larger of the two numbers. To make the comparison easier, extra zeros can be written to the right of the decimal place.

Example:

Compare two positive decimal numbers

1. Which of the two decimals 3.59 and 3.5906 is larger?

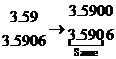since 0 < 6, therefore 3.59 < 3.5906

2. Which of the two decimals 0.009 and 0.01 is larger?

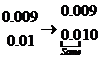since 0 < 1, therefore 0.009 < 0.01

Comparing Negative Decimals

To compare two negative numbers in decimal notation, start at the left and compare corresponding digits moving from left to right. If two digits differ, the number with the smaller digit is the larger of the two numbers.

Example:

Compare two negative decimal numbers

1. Which of the two decimals -5.69 and -5.689 is larger?

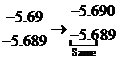since 9 > 8, therefore -5.69 < -5.689

2. Which of the two decimals -0.014 and -0.015 is larger?

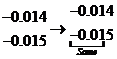since 4 < 5, therefore -0.014 > 0.01

Rounding

Rounding is done exactly the same as for the whole numbers

Rounding Decimal Notation

To round to a certain place:

1. Locate the corresponding digit in that place in the number.

2. Look at the next digit on the right:

a. If this digit is 5 or larger, round up – drop all digits to the right of rounding location and add one to the digit in the rounding place.

b. If this digit less than 5, round down – drop all digits to the right of rounding location, the digit in the rounding place remains unchanged.

Example:

Round the following decimal numbers

1. Round 72.684 to the closest hundredths.

Locate the hundredths digit 72.684

The number to the right is 4, less than 5, round down: drop all the digits to the right of hundredths

2. Round 5052.37 to the closest tenths

Locate the tenths digit 5052.37

The number to the right is 7, greater than 5, round up: add 1 to 3 and drop all the digits to the right